Die MESYS Wälzlagerberechnung gibt Tangentensteifigkeitsmatrizen und Nachgiebigkeitsmatrizen für Wälzlager aus. Ein Beispiel einer Tangentensteifigkeitsmatrix für ein 6204-C3 Rillenkugellager mit einer Radialbelastung von 2 kN wird hier dargestellt:
| ux [µm] | uy [µm] | uz [µm] | ry [mrad] | rz [mrad] | |
| Fx [N] | 6,870908 | 0 | 0 | 0 | -97,8685 |
| Fy [N] | 0 | 124,8287 | 0 | 0 | 0 |
| Fz [N] | 0 | 0 | 54,25732 | 0 | 0 |
| My [Nm] | 0 | 0 | 0 | 0,466423 | 0 |
| Mz [Nm] | -0,09968 | 0 | 0 | 0 | 1,461134 |
Die Tangentensteifigkeit gibt an, um welchen Betrag sich die Belastung bei einer Variation der Relativverschiebung aus dem Arbeitspunkt ändert. Bei einer Axialverschiebung um 1 µm, erhöht sich die Axialkraft um 6.9N und das Kippmoment um die z-Achse vermindert sich um 0.1 Nm. Da das Lager hier rein radial belastet wird, liegt keine Kopplung der Radial- und Axialkomponenten vor. Dies ist bei Radial- und Axialbelastung anders.
Die folgenden Diagramme zeigen die Radialkraft sowie das zweite Hauptdiagonalelement der Tangentensteifigkeitsmatrix über der Radialverschiebung eines 6204-C3 für zwei unterschiedliche Axialverschiebungen.
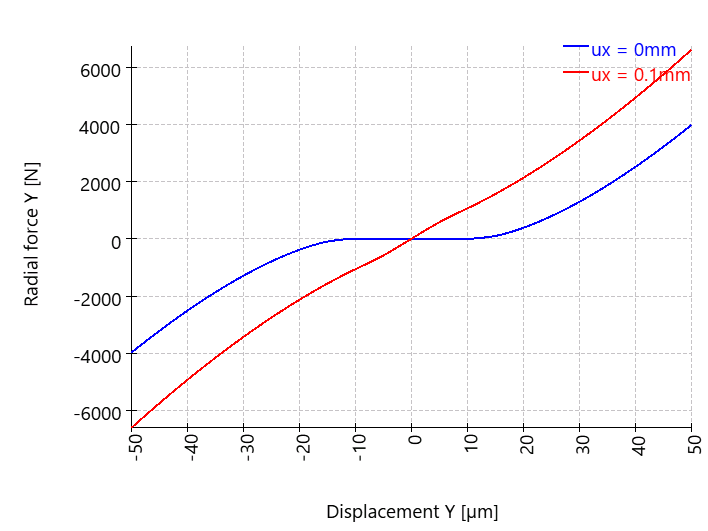
Radialkraft über Radialverschiebung für zwei Axialverschiebungen
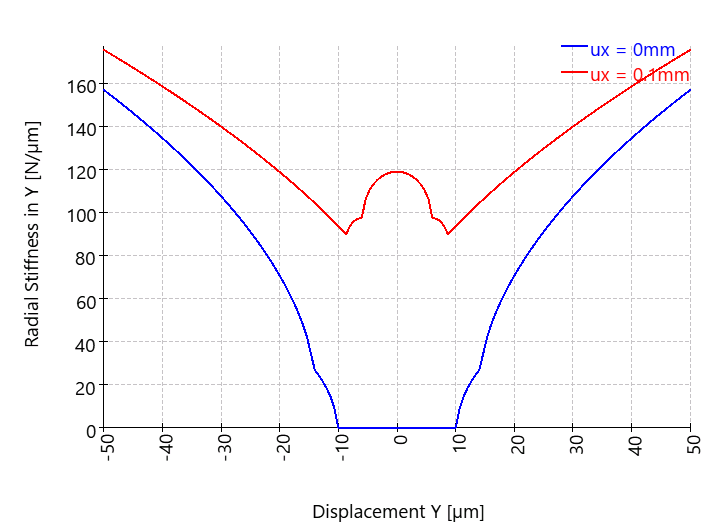
Radiale Steifigkeit über Radialverschiebung für zwei Axialverschiebungen
Da das Rillenkugellager Spiel aufweist, ist die Radialkraft und auch die Radialsteifigkeit teilweise Null. Man sieht, dass der einfache Ansatz Kraft gleich Steifigkeit mal Weg bei nichtlinearen Wälzlagern nicht funktioniert. Der Endpunkt der blauen Kurve ist weit entwert von 155*50 = 7750 N, der Endpunkt der roten Kurve ebenfalls niedriger als 175*50 = 8750 N. Der Grund ist die Nichtlinearität der Lagersteifigkeit.
Der Kraft-Weg-Verlauf des Lagers lässt sich mit der Tangentensteifigkeitsmatrix K so beschreiben:
F(u) = F(u0) + K*(u-u0) = F0 + K*u – K*u0 = K*u + (F0 – K*u0)
Um in einer FE-Berechnung, die korrekte statische Deformation zu bekommen, muss man neben der Tangentensteifigkeitsmatrix noch den Kraftvektor (F0 – K*u0) berücksichtigen, um die Nichtlinearität zu berücksichtigen. Im Falle einer linearen Steifigkeit ist dieser Kraftvektor gerade Null.
Wenn nur Eigenfrequenzen berechnet werden sollen und keine statische Lösung benötigt wird, dann kann man auf den Kraftvektor verzichten. Für eine korrekte statische Lösung ist der Term allerdings erforderlich.


